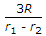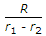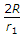|
Directions to Solve
In each question below is given a statement followed by two assumptions numbered I and II. You have to consider the statement and the following assumptions and decide which of the assumptions is implicit in the statement.
Give answer
- (A) If only assumption I is implicit
- (B) If only assumption II is implicit
- (C) If either I or II is implicit
- (D) If neither I nor II is implicit
- (E) If both I and II are implicit.
A
Both I and II are implicit
B
Only assumption I is implicit
C
Either I or II is implicit
D
Only assumption II is implicit
E
Neither I nor II is implicit
ANS:E -
Both I and II are implicit
Explanation:
The stress on 'in their own interest' in the statement indicates that people should use seat belts for their own safety. So, I is implicit. Besides, the announcement has been made to caution passengers to be careful if they want to enjoy a safe ride. So, II is also implicit.
|
ANS:E - NagpurMumbai
No answer description is available. Let's discuss.
|
A
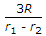
B

C
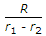
D
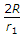
ANS:B -
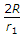
Actual formula = 2R/(r1 - r2).
|
ANS:C -
TE and TM waves
Answer : Option D.
A waveguide is a single conductor with a dielectric inside it (Air is also a dielectric).
TEM mode is characterized by electric fields and magnetic fields perpendicular to one another and perpendicular to the direction of propagation.
In order to have such a configuration, there has to be a source of electric field at the centre from where E fields originate and terminate on the outer conductor and there has to be a current source which can generate magnetic fields.
For TEM mode the current flow should be along the axis of the waveguide, which creates rotating magnetic fields which are normal to the electric fields generated due to the (moving) charges in the current carrying conductor.
Since such a current source is absent and waveguide being a single conductor configuration, TEM mode cannot exist inside a waveguide. Also it is evident from the above explanation that for TEM mode to exist, presence of at least two conductors is compulsory.
|
C
have both their operands in the main store.
D which perform indicated operations on two fast registers of the machine and have the result in one of the registers
E
which perform an operation on a register operand and an operand which is located in the main store, generally leaving the result in the register, expect in the case of store operation when it is also written into the specified storage location.
ANS:A -
have both their operands in the main store.
Memory to Memory Instructions was popular in the 60s and 70s with PDP-8 and PDP-11 ISA. The most recent one I know is VAX-11 ISA that uses their instructions.
They are slow but operate directly on the physical memory, therefore, are simpler to understand.
For reference, you can look up the Instruction Manual for DEC PDP-11 or DEC VAX-11/780.
|
ANS:B - tabling
Gold ore concentration is mostly done using froth flotation.
Here's why:
-
Froth Flotation:
- Froth flotation is a widely used method for separating valuable minerals from their ores.
- In the case of gold ore concentration, froth flotation is particularly effective because gold is often associated with sulfide minerals such as pyrite, and flotation can selectively separate these minerals from the gangue (unwanted material).
- The process involves adding specific reagents (collectors and frothers) to the ore slurry, which creates froth on the surface of the flotation cell. Valuable minerals, including gold-bearing sulfides, attach to the bubbles in the froth and are carried to the surface for recovery.
-
Other Methods:
- Jigging: This method uses pulsating water to separate minerals based on density differences. It is less commonly used for gold ore concentration compared to other methods like gravity separation.
- Tabling: Also known as shaking tables, tabling uses riffles and water flow to separate particles based on density. It is effective for some types of ores but less commonly used for gold ores.
- Elutriation: This method uses fluid flow to separate particles based on size and density. It is more suitable for fine particles and is not typically used for gold ore concentration.
-
Effectiveness and Application:
- Froth flotation is preferred for gold ore concentration due to its high selectivity and efficiency in separating gold-bearing minerals from other minerals and gangue.
- The process can be tailored to optimize recovery rates and concentrate grades based on the specific ore characteristics and processing requirements.
Therefore, froth flotation is the primary method used for gold ore concentration in mining and mineral processing operations.
|
ANS:A - Pakistan
The FIH has withdrawn the hosting rights for the Olympic qualifiers from Pakistan due to security concerns.
|
ANS:C -
Mali
In Mali, the military has appointed Colonel Abdoulaye Maiga as interim Prime Minister after the country's civilian PM Choguel Kokalla Maiga was admitted to hospital.
|
ANS:C - second
A mercury manometer (U-tube type) exemplifies a first-order system.
In a first-order system, the response of the system to a change in input is proportional to the first derivative of the output. For a mercury manometer, the height of the mercury column responds to pressure changes in a manner consistent with a first-order system, where the rate of change of the mercury height is proportional to the difference between the current height and the equilibrium height. This is analogous to the behavior of other first-order systems such as RC (resistor-capacitor) circuits and thermal systems.
A mercury manometer (U-tube type) exemplifies a first-order system due to the way it responds to changes in pressure. Here’s a detailed explanation:
-
System Description:
- A U-tube manometer consists of a U-shaped tube filled with mercury (or another liquid).
- One end of the U-tube is open to the atmosphere, and the other end is connected to the pressure source to be measured.
- When there is a pressure difference between the two ends, the mercury levels in the two arms of the U-tube change until they reach a new equilibrium.
-
First-Order System Characteristics:
- A first-order system is characterized by a single energy storage element, which, for the manometer, is the potential energy of the mercury column.
- The response of a first-order system to a step input (sudden change in pressure) is an exponential function, which describes how the system gradually approaches its new equilibrium position.
-
Dynamic Response:
- When there is a sudden change in pressure, the mercury in the U-tube moves until the pressure difference is balanced by the height difference of the mercury columns.
- The rate at which the mercury moves is initially fast and then slows down as it approaches the new equilibrium. This behavior is typical of a first-order response.
- The time constant (τ\tauτ) for the mercury manometer depends on factors like the density of mercury, the viscosity of mercury, and the geometry of the U-tube. The time constant describes how quickly the mercury column reaches 63.2% of the total height change after a sudden pressure change.
-
Mathematical Representation:
- If h(t)h(t)h(t) represents the height difference between the two columns at time ttt, the first-order differential equation describing the system might look like: τdh(t)dt+h(t)=KΔP\tau \frac{dh(t)}{dt} + h(t) = K \Delta Pτdtdh(t)+h(t)=KΔP where ΔP\Delta PΔP is the pressure difference, KKK is a constant related to the system's sensitivity, and τ\tauτ is the time constant.
- This equation shows that the rate of change of the height difference (dh(t)/dtdh(t)/dtdh(t)/dt) is proportional to the difference between the current height and the equilibrium height, which is a hallmark of first-order systems.
-
Practical Implications:
- Understanding that the mercury manometer behaves as a first-order system helps in predicting its behavior in response to pressure changes.
- For example, if you know the time constant, you can estimate how quickly the manometer will settle to its new reading after a change in pressure.
In summary, a mercury manometer exemplifies a first-order system due to its exponential response to changes in pressure, characterized by a time constant that governs the speed of its response. This behavior is similar to other first-order systems where a single energy storage element determines the system's dynamic response.
|
ANS:C - second
A mercury manometer (U-tube type) exemplifies a first-order system.
In a first-order system, the response of the system to a change in input is proportional to the first derivative of the output. For a mercury manometer, the height of the mercury column responds to pressure changes in a manner consistent with a first-order system, where the rate of change of the mercury height is proportional to the difference between the current height and the equilibrium height. This is analogous to the behavior of other first-order systems such as RC (resistor-capacitor) circuits and thermal systems.
A mercury manometer (U-tube type) exemplifies a first-order system due to the way it responds to changes in pressure. Here’s a detailed explanation:
-
System Description:
- A U-tube manometer consists of a U-shaped tube filled with mercury (or another liquid).
- One end of the U-tube is open to the atmosphere, and the other end is connected to the pressure source to be measured.
- When there is a pressure difference between the two ends, the mercury levels in the two arms of the U-tube change until they reach a new equilibrium.
-
First-Order System Characteristics:
- A first-order system is characterized by a single energy storage element, which, for the manometer, is the potential energy of the mercury column.
- The response of a first-order system to a step input (sudden change in pressure) is an exponential function, which describes how the system gradually approaches its new equilibrium position.
-
Dynamic Response:
- When there is a sudden change in pressure, the mercury in the U-tube moves until the pressure difference is balanced by the height difference of the mercury columns.
- The rate at which the mercury moves is initially fast and then slows down as it approaches the new equilibrium. This behavior is typical of a first-order response.
- The time constant (τ\tauτ) for the mercury manometer depends on factors like the density of mercury, the viscosity of mercury, and the geometry of the U-tube. The time constant describes how quickly the mercury column reaches 63.2% of the total height change after a sudden pressure change.
-
Mathematical Representation:
- If h(t)h(t)h(t) represents the height difference between the two columns at time ttt, the first-order differential equation describing the system might look like: τdh(t)dt+h(t)=KΔP\tau \frac{dh(t)}{dt} + h(t) = K \Delta Pτdtdh(t)+h(t)=KΔP where ΔP\Delta PΔP is the pressure difference, KKK is a constant related to the system's sensitivity, and τ\tauτ is the time constant.
- This equation shows that the rate of change of the height difference (dh(t)/dtdh(t)/dtdh(t)/dt) is proportional to the difference between the current height and the equilibrium height, which is a hallmark of first-order systems.
-
Practical Implications:
- Understanding that the mercury manometer behaves as a first-order system helps in predicting its behavior in response to pressure changes.
- For example, if you know the time constant, you can estimate how quickly the manometer will settle to its new reading after a change in pressure.
In summary, a mercury manometer exemplifies a first-order system due to its exponential response to changes in pressure, characterized by a time constant that governs the speed of its response. This behavior is similar to other first-order systems where a single energy storage element determines the system's dynamic response.
|