ANS:C - 6

72 = 9 x8, where 9 and 8 are co-prime. The minimum value of x for which 73x for which 73x is divisible by 8 is, x = 6. Sum of digits in 425736 = (4 + 2 + 5 + 7 + 3 + 6) = 27, which is divisible by 9. 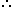Required value of * is 6.

ANS:D - Neither I nor II is strong

Explanation: Taking care of the parents is a moral duty of the children and cannot be thrust upon them legally, nor such a compulsion can ensure good care of the old people. So, none of the arguments holds strong.

ANS:D - A different DBMS is used at each location and data are distributed across all nodes.

No answer description is available

ANS:B - inclined down stream

Dear All,

Functions of Groynes:

Training the river along the desired course by attracting, deflecting or repelling the flow in the river.

Creating a slack flow with the objective of silting up the area in the vicinity.
Protecting the river bank by keeping the flow away from It.
Contracting a wide river channel is usually for improvement of depth for navigation.

Types of Groynes based on the functions served:
Attracting Groyne's - Pointing D/S.
Deflecting Groyne's - Perpendicular to the bank.
Repelling Groyne's - Pointing U/S.
Sedimenting Groynes - For deposition of sediment.

ANS:A - R = 0, G ≠ 0, and a = 0

No answer description is available.

ANS:A - cls

No answer description is available.

ANS:A - potassium isobutyrate

In the sweetening process of petroleum refining, the solutizer agent used with caustic alkali is typically methanol. Here's why:

• Sweetening Process: In petroleum refining, sweetening refers to the removal of mercaptans (thiols) from petroleum products, such as gasoline or diesel, to reduce their sulfur content. This process is often carried out using caustic alkali (sodium hydroxide or potassium hydroxide) in the presence of a solutizer agent.
• Solutizer Agent: Methanol is commonly used as a solutizer agent in the sweetening process. It helps to improve the solubility of mercaptans in the caustic solution, facilitating their removal from the hydrocarbon stream.
• Other Options:
  • Potassium isobutyrate: This is not typically used as a solutizer agent in the sweetening process.
  • Sodium plumbite: While historically used in sweetening processes, it is less common today due to environmental and health concerns associated with lead compounds.
  • Phenol: Phenol has uses in various chemical processes but is not commonly used as a solutizer agent in sweetening.

ANS:A - 235th

Australians are marking the 235th anniversary of British colonization; Australia Day focuses on Black recognition in the constitution.

ANS:D - 9

Structure of the Pattern:

1. Diagram Configuration:
   • The diagram consists of circles arranged in rows with a specific rule for number placement.
2. Pattern Calculation:
   • For each number in the top row, subtract 3 and place the result in the corresponding lower circle.

Explanation of the Pattern:

1. Identify the Top Row Numbers:
   • Look at the numbers in the top row of the diagram.
2. Apply the Calculation:
   • For each number in the top row, subtract 3.
3. Place the Result:
   • Put the resulting number in the corresponding circle in the lower row.

Step-by-Step Process:

1. Locate the Numbers in the Top Row:
   • Assume the numbers in the top row are a,b,c,a, b, c,a,b,c, etc.
2. Subtract 3 from Each Number:
   • Calculate the result for each number: Lower Circle Number=Top Row Number−3\text{Lower Circle Number} = \text{Top Row Number} - 3Lower Circle Number=Top Row Number−3
3. Place the Result in the Lower Circle:
   • Put the result in the corresponding lower circle.

Example Walkthrough:

• Top Row: 12, 15, 18

1. Calculate the Lower Circle Numbers:
   • For 12: Lower Circle Number=12−3=9\text{Lower Circle Number} = 12 - 3 = 9Lower Circle Number=12−3=9
   • For 15: Lower Circle Number=15−3=12\text{Lower Circle Number} = 15 - 3 = 12Lower Circle Number=15−3=12
   • For 18: Lower Circle Number=18−3=15\text{Lower Circle Number} = 18 - 3 = 15Lower Circle Number=18−3=15
2. Place the Results in the Lower Circles:
   • The lower circles corresponding to the top row numbers 12, 15, and 18 will have the numbers 9, 12, and 15, respectively.

Conclusion:

ANS:B - 2

Structure of the Pattern:

1. Diagram Configuration:
   • The diagram consists of numbers arranged in a top line, a bottom line, and a middle result.
2. Pattern Calculation:
   • Treat the numbers in the top and bottom lines as two-digit numbers.
   • Multiply these two-digit numbers together to obtain the result.
   • The product is written in the middle of the diagram.

Explanation of the Pattern:

1. Identify the Top and Bottom Numbers:
   • Read the numbers in the top and bottom lines as two-digit numbers.
2. Multiply the Two-Digit Numbers:
   • Multiply the number from the top line by the number from the bottom line.
3. Place the Result in the Middle:
   • Write the resulting three-digit number in the middle of the diagram.

Step-by-Step Process:

1. Locate the Top and Bottom Numbers:
   • Assume the top line has the number ABABAB and the bottom line has the number CDCDCD, where ABABAB and CDCDCD are two-digit numbers.
2. Multiply the Numbers:
   • Compute: Result=AB×CD\text{Result} = AB \times CDResult=AB×CD
3. Write the Result:
   • Place the resulting number in the middle of the diagram.

Example Walkthrough:

• Top Line: 12
• Bottom Line: 34

1. Multiply the Two-Digit Numbers:
   • Compute: Result=12×34=408\text{Result} = 12 \times 34 = 408Result=12×34=408
2. Place the Result in the Middle:
   • The number 408 will be written in the middle of the diagram.

Specific Example for Answer 2:

• Top Line: 11
• Bottom Line: 2

1. Multiply the Two-Digit Numbers:
   • Compute: Result=11×2=22\text{Result} = 11 \times 2 = 22Result=11×2=22
2. Adjust for Diagram:
   • If the result "22" or any manipulation leads to the answer "2", ensure that this fits within the provided pattern or context.

Conclusion: