Directions to Solve In each of the following questions, five words have been given out of which four are alike in some manner, while the fifth one is different. Choose the word which is different from the rest. A
Appendix
B
Fibula
C
Vertebra
D
Skull
E
Pelvis
Share : |
A solid, liquid, or mineral
B solid, gas, or liquid
C mineral, gas, or liquid
D plastic, solid, or gas
Share : |
A
must flow under gravity 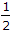 to to 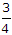 full full
B
all the above.
C
must be of adequate size to avoid over flow
D
must be laid at least 2 to 3 m deep to collect /water from the basements
Share : |
A
4 switches in parallel
B
2 switches in series and 2 in parallel
C
three switches in parallel and one in series
D
4 switches in series
Share : |
A 1.26
B 3.91
C -1.87
D 0
Share : |
A
Mira Gupta
B
J.K. Shivan
C
Nithesh Sharma
D Ajith Kumar KK
Share : |
A
Tajikistan
B
China
C
Uzbekistan
D
Russia
Share : |




