img not found img not found

Ratio and Proportion

  1. Ratio: The ratio of two quantities a and b in the same units, is the fraction 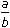and we write it as a : b. In the ratio a : b, we call a as the first term or antecedent and b, the second term or consequent.
    Eg. The ratio 5 : 9 represents 5 with antecedent = 5, consequent = 9.
    9
    Rule: The multiplication or division of each term of a ratio by the same non-zero number does not affect the ratio. Eg. 4 : 5 = 8 : 10 = 12 : 15. Also, 4 : 6 = 2 : 3.
  2. Proportion: The equality of two ratios is called proportion. If a : b = c : d, we write a : b :: c : d and we say that a, b, c, d are in proportion. Here a and d are called extremes, while b and c are called mean terms. Product of means = Product of extremes. Thus, a : b :: c : d (b x c) = (a x d).
  3. Fourth Proportional:If a : b = c : d, then d is called the fourth proportional to a, b, c.Third Proportional:a : b = c : d, then c is called the third proportion to a and b.Mean Proportional:Mean proportional between a and b is ab.
  4. Comparison of Ratios:
    We say that (a : b) > (c : d) a > c .
    b d
    Compounded Ratio: The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).
  5. Duplicate Ratios: Duplicate ratio of (a : b) is (a2 : b2). Sub-duplicate ratio of (a : b) is (a : b). Triplicate ratio of (a : b) is (a3 : b3). Sub-triplicate ratio of (a : b) is (a1/3 : b1/3).
    If a = c , then a + b = c + d . [componendo and dividendo]
    b d a - b c - d
  6. Variations: We say that x is directly proportional to y, if x = ky for some constant k and we write, x y. We say that x is inversely proportional to y, if xy = k for some constant k and
    we write, x 1 .
    y



img not found
img

For help Students Orientation
Mcqs Questions

One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.