

Hydraulics - Engineering
Q1: Euler's equation for motion of liquids, is given byA

B
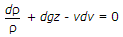
C
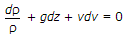
D
ρdp + gdz + vdv = 0
ANS:C -
Euler's equation for the motion of liquids is a fundamental equation in fluid dynamics that describes the motion of an inviscid (non-viscous) fluid in the absence of external forces. It is derived from Newton's second law of motion applied to fluid elements. Euler's equation, expressed in vector form, is: ∂v/∂t+(v⋅∇)v=−1/p∇p+g Where:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

