- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 2
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 22


Exam Questions Papers - Engineering
Q1:
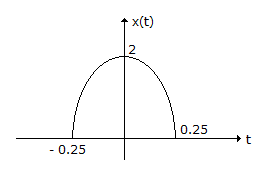 |


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.


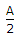 [δ(f - f0) + δ(f + f0)]
=
[δ(f - f0) + δ(f + f0)]
= 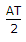 [sin c [T(f - f0)] + sin c[T(f + f0)]]
[sin c [T(f - f0)] + sin c[T(f + f0)]]
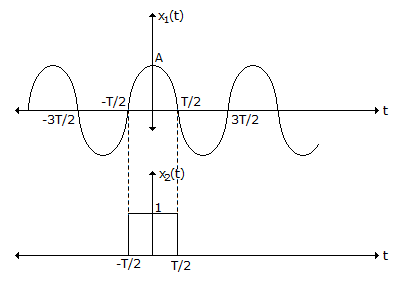 Now, A = 2, T = 0.5 and f0 =
Now, A = 2, T = 0.5 and f0 =  = 1
=> X(f) = 0.5[sin c (0.5(f - 1)) + sin c (0.5(f + 1))].
= 1
=> X(f) = 0.5[sin c (0.5(f - 1)) + sin c (0.5(f + 1))].