Q1: Given digits 2, 2, 3, 3, 3, 4, 4, 4, 4 how many distinct 4 digit numbers greater than 3000 can be formed?

The given digits are 2, 2, 3, 3, 3, 4, 4, 4, 4 we have to find the numbers that are greater than 300 ∴ The first digit can be 3 or 4 but not 2. Now, let us fix the first, second and third digits as 3, 2, 2, then the fourth place can be filled in 3 ways. 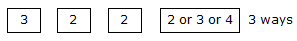∴ The number of ways is 3 similarly, we fix first third and fourth place as 3, 2 and 2 respectively (4) so the second place can be filled in 3 ways again, 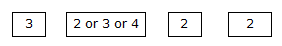The number of ways is 3 Now, we fix first, second and fourth, previous cases and we obtain the same result. ∴ The number of ways is 3 so, the total number of ways is 9 similarly this can done by fixing the numbers as 3 and 4 (instead of 2) and thereby we obtain the a ways each The number of numbers starting with 3 is 27 Similarly by taking 4 as the first digit we get 27 numbers ∴ The number of numbers that are greater than 3000 is 27 + 27 = 54 But, 3222, 4222, is not possible as there are only two 2's, 3333 is not possible as there are only three 3's ∴ The total number of numbers that are greater than 3000 is 54 - 3 = 51.