

RCC Structures Design - Engineering
Q1: If d and n are the effective depth and depth of the neutral axis respectively of a singly reinforced beam, the lever arm of the beam, isA
d
B
n
C
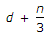
D
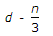
E
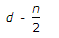
ANS:D -
The lever arm (x) of a singly reinforced beam is the distance from the centroid of the compressive force block to the centroid of the tensile force block. It's a crucial parameter in determining the bending moment and the distribution of stresses in the beam. The lever arm (x) can be calculated using the formula: 3x=d−3n Where:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

