

RCC Structures Design - Engineering
Q1: If l1 and l2 are the lengths of long and short spans of a two way slab simply supported on four edges and carrying a load w per unit area, the ratio of the loads split into w1 and w2 acting on strips parallel to l2 and l1 isA 
B 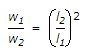
C 
D 
ANS:D - To determine the loads split into w1 and w2 acting on strips parallel to l2 and l1, respectively, we can use the principle of the equivalent frame method for analyzing two-way slabs. This method assumes that the slab behaves as a series of parallel beams in two directions. Let's denote:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

