

RCC Structures Design - Engineering
Q1: If permissible compressive stress in concrete is 50 kg/cm2, tensile stress in steel is 1400 kg/cm2 and modular ratio is 18, the depth d of the beam, isA 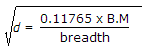
B 
C 
D 
E 
ANS:A - To determine the depth (d) of the beam, we can use the concept of modular ratio (m) in reinforced concrete beam design. The modular ratio (m) relates the modulus of elasticity of steel (Es) to the modulus of elasticity of concrete (Ec) and is given by: m=Ec/Es Given that the modular ratio (m) is 18, we can express the modulus of elasticity of steel (Es) in terms of the modulus of elasticity of concrete (Ec): Es=m×Ec Now, we know that the tensile stress in steel (σs) can be related to the compressive stress in concrete (σc) through the modular ratio: σs=m×σc Given that the permissible compressive stress in concrete (σc) is 50 kg/cm² and the tensile stress in steel (σs) is 1400 kg/cm², we can rearrange the equation to solve for the compressive stress in concrete: σc=σs/m σc=(1400kg/cm2)/18 σc≈77.78kg/cm^2 Now, we can use the formula for compressive stress in concrete to find the depth (d) of the beam: σc=M/Z Where:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

