

RCC Structures Design - Engineering
Q1: If W is the load on a circular slab of radius R, the maximum circumferential moment at the centre of the slab, isA
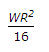
B
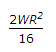
C
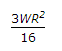
D
zero
E
none of these.
ANS:C -
The maximum circumferential moment at the center of a circular slab subjected to a uniformly distributed load W can be calculated using basic principles of structural mechanics. This moment occurs at the center of the circular slab and represents the maximum bending moment induced by the applied load. The formula to calculate the maximum circumferential moment (maxMmax) at the center of a circular slab subjected to a uniformly distributed load is given by: Mmax=2W⋅R Where:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

