

Permutation and Combination - General Aptitude
Q1: In how many different ways can the letters of the word 'CORPORATION' be arranged so that the vowels always come together?A 810
B 1440
C 2880
D 50400
E 5760
ANS:D - 50400 In the word 'CORPORATION', we treat the vowels OOAIO as one letter. Thus, we have CRPRTN (OOAIO). This has 7 (6 + 1) letters of which R occurs 2 times and the rest are different.
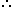 Required number of ways = (2520 x 20) = 50400. Required number of ways = (2520 x 20) = 50400.
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

