

Hydraulics - Engineering
Q1: Inside pressure in a hollow soap bubble in the air is : (where d is the diameter of the bubble)A
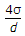
B
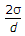
C
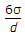
D
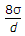
ANS:D -
The expression 8σ/d represents the inside pressure in a hollow soap bubble in the air, where σ is the surface tension of the soap solution and d is the diameter of the bubble. The formula is derived from the Young-Laplace equation, which describes the relationship between the pressure inside a curved liquid interface (such as a soap bubble) and the surface tension of the liquid and the curvature of the interface. The Young-Laplace equation states: P = 2σ/r Where:
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

