

Applied Mechanics - Engineering
Q1: Pick up the correct statement from the following :A
If two equal and perfectly elastic smooth spheres impinge directly, they interchange their velocities.
B
If a sphere impinges directly on an equal sphere which is at rest, then a fraction 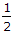 (1 - e2) the original kinetic energy is lost by the impact. (1 - e2) the original kinetic energy is lost by the impact.
C
If a smooth sphere impinges on another sphere, which is at rest, the latter will move along the line of centres.
D
If two equal spheres which are perfectly elastic impinge at right angles, their direction after impact will still be at right angles.
E
All the above.
ANS:E - All the above.
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

