- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 2
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 22


Exam Questions Papers - Engineering
Q1: The autocorrelation function of an ergodic random process is given by __________ .A 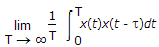 B 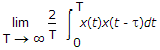 C 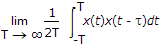 D 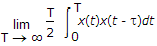 ANS:C - 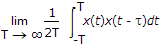
The expectations or ensemble average of a random process x(t) are averages "across the process".
The DC value of x(t) is defined by the time average
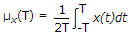 The other time average of particular interest is the autocorrelation function Rx(t, T) defined in terms of the sample function x(t) observed over the interval - T ≤ t ≤ T.
Following equation, we may formally define the time-averaged autocorrelation function of a sample function x(t) as follows :
The other time average of particular interest is the autocorrelation function Rx(t, T) defined in terms of the sample function x(t) observed over the interval - T ≤ t ≤ T.
Following equation, we may formally define the time-averaged autocorrelation function of a sample function x(t) as follows :
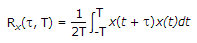 This second time-average should also be viewed as a random variable with a mean and variance of its own.
In a manner similar to ergodicity of the mean, we say that the process x(t) is ergodic in the autocorrelation function if the following two limiting conditions are satisfied :
This second time-average should also be viewed as a random variable with a mean and variance of its own.
In a manner similar to ergodicity of the mean, we say that the process x(t) is ergodic in the autocorrelation function if the following two limiting conditions are satisfied :
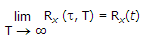
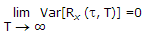 . .
|


For help Students Orientation
Mcqs Questions
One stop destination for examination, preparation, recruitment, and more. Specially designed online test to solve all your preparation worries. Go wherever you want to and practice whenever you want, using the online test platform.

