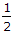The masses of two balls are in the ratio of 2 : 1 and their respective velocities are in the ratio of 1 : 2 but in opposite direction before impact. If the coefficient of restitution is , the velocities of separation of the balls will be equal to

ANS:D - original velocity in the opposite direction

In Question Given that opposite direction i.e head on Collision.

Let m1, u1 for 1st body moving towards second body and
m2,u2 for a second body moving towards 1st body

Therefore after colliding final velocities are v1 & v2 respectively
As per the law of conservation:

Initial change in momentum = Final change in momentum
m1u1-m2u2 = m2v2-m1v1.
2m2u1-m2u2 = m2v2-2m2v1 (given m1=2m2).
m2(2u1-u2) = m2(v2-2v1).
2u1-2u1 = v2-2v1 (given u2=2u1).
0 = v2-2v1.
v1/v2 = 1/2 ie equal to ratio of original velocity.

So, Option D is correct. The mass of 1st ball (m1)=2M, mass of 2nd ball (m2)= M
initial velocity of 1st ball (u1)= U, initial velocity of 2nd ball (u2)= -2U { -ve sign because of opp direction.

The coefficient of restitution=1/2,
let, v1 = final velocity of 1st ball, v2= final velocity of the 2nd ball
from the law of conservation of momentum,
m1u1+m2u2=m1v1+m2v2.
2MU+M(-2U)=2Mv1+Mv2.
0=2Mv1+Mv2.
v2=-2v1.

From the law of collision of elastic bodies that;
(v2-v1)=e(u1-u2).
On solving v1=-1/2 U.

So negative sign indicates that the direction of v1 is opposite to that of U thus 1st ball will move back with 1/2 of its original velocity.